Gewinnschwelle, umsatzbezogen Weiter Zurück Schließen Die umsatzbezogene Gewinnschwelle (Break-even-Point, siehe Break-even-Analyse) kann graphisch und rechnerisch bestimmt werden: Für die graphische Lösung wählt man ein x,y-Diagramm, wobei auf der x-Achse der Umsatz U [Mio. EUR] und auf der y-Achse die Umsatzerlöse E [Mio. EUR] sowie die Kosten K [Mio. EUR] abgetragen werden. Wenn davon ausgegangen werden kann, dass die Umsätze U ohne Erlösschmälerungen zu Erlösen E transferiert werden, kann die sog. Erlöskurve E = f (U) als Gerade mit einem Abstieg von 45o ins das Diagramm eingetragen werden. Die Fixkostenkurve fK = f (U) ist eine Parallele zur x-Achse, während die Kurve der variablen Kosten vK = f (U) als eine Gerade mit dem Anstieg von a/100 * U, also 0,6 * U, in das Diagramm einzutragen ist. Die Gesamtkostenkurve K = f (U) beginnt bei U = 0 Mio. EUR auf der y-Achse beim Wert der Fixkosten fK und verläuft dann im Weiteren parallel zur Kurve der variablen Kosten. Der Break-even-Point ist jener Punkt im x, y - Diagramm, bei dem die Gesamtkostenkurve K = f (U) die Erlöskurve E = f (U) schneidet, denn hier gilt Erlöse E = Kosten K = Umsatz U. Die Gewinnschwellenwerte sind auf der x-Achse dort abzulesen, wo ein Lot vom Break-even-Point die x-Achse schneidet. Es kann im betrachteten Beispiel der Wert U = 7,5 Mio. EUR abgelesen werden. Die mit dieser Umsatzgröße verbundenen Erlöse E und Kosten K sind auf der y-Achse dort abzulesen, wo eine in Höhe des Break-even-Points gezogene Gerade die y-Achse scheidet. Es können die Werte E = K = 7,5 Mio. EUR abgelesen werden. Rechnerische Bestimmung: Aus dem Ansatz, dass am Break-even-Point die umsatzbezogenen Erlöse E genau den Gesamtkosten K entsprechen, folgt zunächst: Erlöse E = Kosten K = Fixkosten FK + variable Kosten vK = Umsatz U.       (1) Aufgrund einer naheliegenden Annahme, dass sich die variablen Kosten in einem größeren Wertebereich proportional zum Umsatz U verhalten, benötigen wir die Angabe, wie hoch im Durchschnitt der Anteil der variablen Kosten vK am Umsatz U sind. Ist dieser Anteil mit einer Größe a [%] bestimmt, kann die obige Gleichung (1) auch wie folgt geschrieben werden: Erlöse E = Fixkosten fK + a * Umsatz U / 100 = Umsatz U.     (2) Die Gleichung (2) gilt es nach der gesuchten Größe U umzustellen. Zu diesem Zweck sind beide Seiten zunächst mit 100 zu multiplizieren. Wir erhalten: fK * 100 + a * U = U * 100. 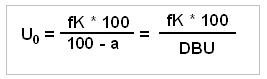Wird diese Gleichung nach der Größe U umgestellt, erhalten wir folgende Bestimmungsgleichung für die Ermittlung der umsatzbezogenen Gewinnschwelle: Es bedeuten: U0      Break-even-Umsatz [EUR], fK       Fixkosten des Unternehmens [EUR], a        Anteil der variablen Kosten am Umsatz [%], DBU   prozentualer Deckungsbeitrag des Umsatzes [%] mit DBU = 100 - a.